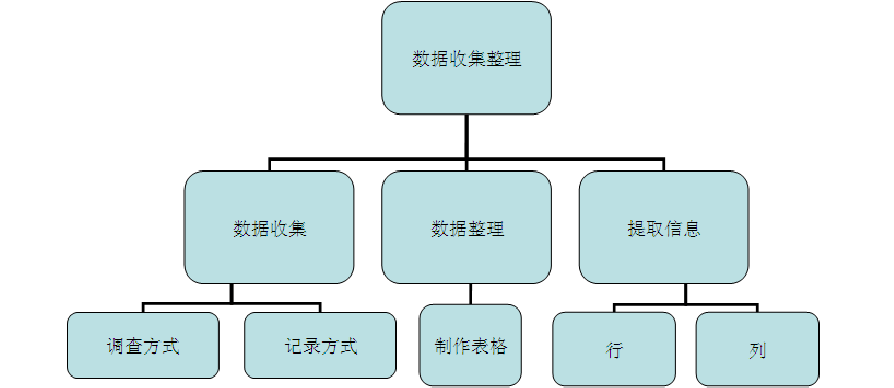
五边形的分析图叫什么?
雷达图。

是用来比较每个数据相对中心点的数值变化,将多个数据的特点以“蜘蛛网”形式呈现出来的图表,多使用倾向分析和把握重点。在商业领域中,雷达图主要被应用在与其他对手的比较、公司的优势和广告调查等方面,主要包括雷达图、带标记的雷达图、填充雷达图。
主成分分析图怎么解析?
主成分分析图可以通过以下三个步骤进行解析。
首先,明确结论是主成分分析图能够展示出数据集中多个变量之间的相关性,同时可以确定哪些变量更重要。
其次,解释原因是主成分分析图是通过将多个变量重构为几个主成分来实现对数据集的降维操作。
在这个过程中,主成分所包含的变量的权重越大,说明这些变量在数据集中的重要性越高,对应的主成分也就越重要。
最后,内容延伸可以包括对主成分分析的应用,如通过主成分分析找到数据集中的模式,进行数据可视化和分类等。
同时还可以探究主成分分析的优缺点,以及如何针对数据集的特征和目的进行参数设置和模型的优化等。
主成分分析(PCA)图是根据数据集中的各个观测变量(称为原始变量)计算的主成分分析结果,通常用于研究或比较不同样本之间的相似性和差别。下面是一个简单的解析步骤:

1. 解释变异性:在一个主成分分析图中,横轴表示第一主成分的得分,纵轴表示第二主成分的得分。因此,首先需要解释第一主成分和第二主成分的得分。第一主成分表现了数据中最大的可解释变异性,即尽可能多地保留原数据的信息。第二主成分有次之,依此类推。
2. 观察聚类:在主成分分析图中,不同样本点的聚类情况通常比较明显,某些样本点会聚集在一起,形成一些群集或者簇。这说明这些样本点在主成分上的得分比较相近,可以用于分类或聚类分析。
3. 解释变量之间的关系:除了观察样本点的聚类情况以外,主成分分析还可以用来解释不同变量之间的关系。如果某些原始变量在主成分上的得分比较高,说明它们在主成分上有很强的相关性,可以通过主成分分析来减少变量数量,简化数据的分析和解释。

4. 评估解释度:通常可以通过观察在主成分分析图中各个主成分所占的方差来评估PCA的解释度,即每个主成分所能解释数据中的变异程度。如果主成分所占的方差比较大,说明这个主成分能够更好地解释数据中的信息。
总的来说,主成分分析图可以很直观地反映数据中的聚类、相关性和变异等信息,通过对主成分分析图的观察和解析可以对样本或者变量之间的差异进行评估和解释。
主成分分析(PCA)是一种常用的数据降维技术,它通过将高维数据投影到低维空间,来减少数据的复杂度。主成分分析图通常是用于可视化数据降维后的结果。下面是解析主成分分析图的一些步骤:
1. 查看贡献率:主成分分析通常会返回一列主成分,每个主成分都有一定的贡献率。贡献率越高的主成分表示这个主成分所解释的数据方差越大。因此,查看每个主成分的贡献率是了解数据降维后特征重要性的重要步骤。
2. 观察主成分之间的关系:主成分之间可能存在一定的相关性,因为它们都是从原始数据中提取出来的。因此,可以通过观察主成分之间的关系,来了解数据的内在结构。
3. 查看数据点在主成分轴上的投影:主成分分析将原始数据投影到低维空间,因此在主成分图中可以看到每个数据点在每个主成分轴上的投影。这可以帮助我们了解数据点在不同主成分上的特征表现,以及它们在低维空间中的分布情况。
4. 分析异常点:在主成分图中,可能会出现一些与其他数据点有明显差异的异常点。这些异常点可能是由于测量误差、数据缺失或极端值等原因引起的。因此,分析异常点可以帮助我们了解数据的可靠性和一致性。
到此,以上就是小编对于数据分析图有哪些图的问题就介绍到这了,希望介绍的2点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏